Before we put together all what we discussed in previous entries, it is worth two spend a few words about how roll stiffness affects load transfer. We said that, the higher the roll stiffness of the front axle with respect to the rear, the higher the load transfer portion that the front axle will experience.
Why this is the case is something that is for some people hard to understand, because they mix up load transfer and roll. Anyway, why the axle with higher roll stiffness will transfer a bigger load than the axle with less (assuming all other conditions staying the same) can be easily understand remembering that we assume the two axes being connected by an ideally rigid chassis. This if, of course, an approximation, but it helps to explain this concept. Moreover, race cars chassis (above all carbon fibers monocoques) are normally very stiff, much stiffer than cars suspensions, so we can assume them being ideally stiff in a first approximation.
Basing on this assumption, we can imagine a car as a bar, connected to the ground by two torsion springs, one at the front and on at the rear axle.

The two torsion springs at the two extreme points of our bar are representative of each suspension roll stiffness, which depends on the effects of springs, antiroll bars and track width, just to name a few. We will come to this later.
This case is analogous to having a perfectly rigid bar lying on two coil, linear springs and being allowed to move only vertically (i.e. having only one degree of freedom) under the action of a vertical force N.

We assume the two springs having two different stiffness, K1 and K2. Since the bar is assumed to be ideally stiff and can only translate vertically, the vertical deflection of the two springs must be the same, so that the bar stays horizontal with respect to the ground. Since the stiffness of the two springs are different, but their deflection is the same, the stiffer spring will experience a bigger force, because said force is directionally proportional to stiffness and deflection, as per the following equation:
![]()
Where “x” is spring deflection from its initial/free length position.
The sum of the forces experienced by each spring will be equal to the vertical force N we initially applied to the bar.
What happens with a real car is exactly the same, with the only exception that we deal with a rotational stiffness (spring) instead of a linear one, that the only motion (degree of freedom) that we consider is car roll and that, in place of the horizontal bar we have car chassis (assumed to be ideally rigid).
The force experienced by each of our springs corresponds to roll moment experienced by each axle, under the influence of its roll stiffness. Roll moment and load transfer are strictly linked (through axle track width). The higher the axle torsional stiffness with respect to the other, the higher the portion of the load transfer that axle will absorb.
The roll stiffness of a suspension can be calculated basing on the effect at the contact patch of (corner) springs and antiroll bar stiffness, as we said. It is important to stress that here we only and always refer to the effects “at ground” of spring and antiroll bar stiffness, also usually named wheel rates.
In a roll situation, the stiffness of a spring and of the antiroll bar on the wheel rate can be calculated summing the two together, as the two components act as two springs in parallel.
The final roll stiffness of the axle, anyway, is also influenced by tyre stiffness and can be calculated using the following equation:

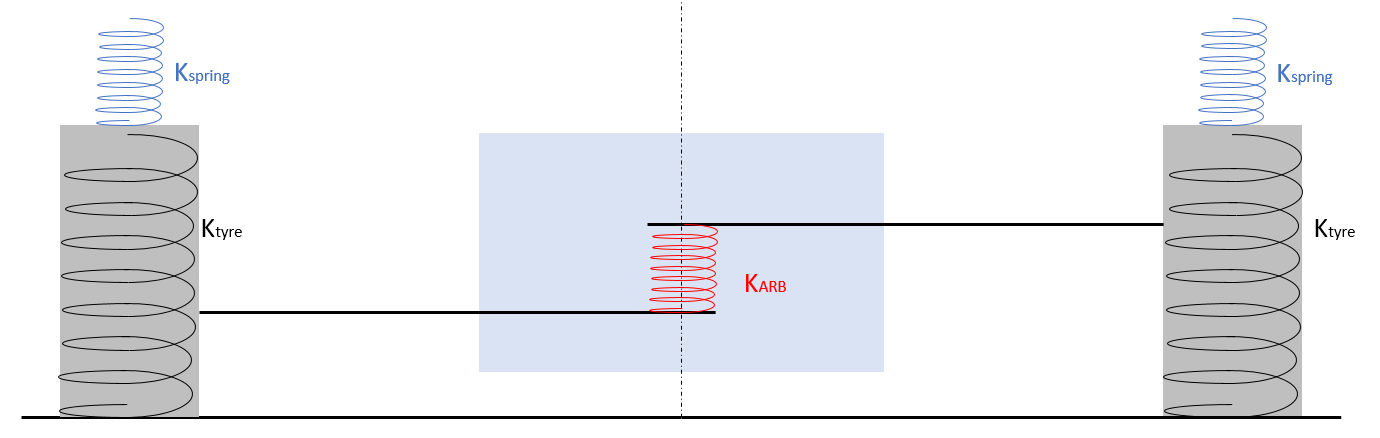
Where:
Kroll is the final roll stiffness of the axle we consider (Nm/rad);
Kspring is the roll wheel rate portion coming from the spring (N/mm);
KARB is the roll wheel rate portion coming from the antiroll bar (N/mm);
Ktyre is the roll wheel rate portion coming from the antiroll bar (N/mm);
Tr is the axle track width.
As we mentioned, the load transfer each axle experiences can be divided in a sprung and unsprung mass contribution. Anyway, since we have seen that the unsprung mass load transfer is not a tunable parameter and to keep our analysis as easy as possible, we will simply incorporate its contribution in the overall axle load transfer. Anyway, one thing to mention (and that many books don’t explore) is that the unsprung mass has also an influence on the roll angle (although often small), because the forces the unsprung mass experiences (think for example to a wheel assembly) will be transmitted to the chassis through the control arms.
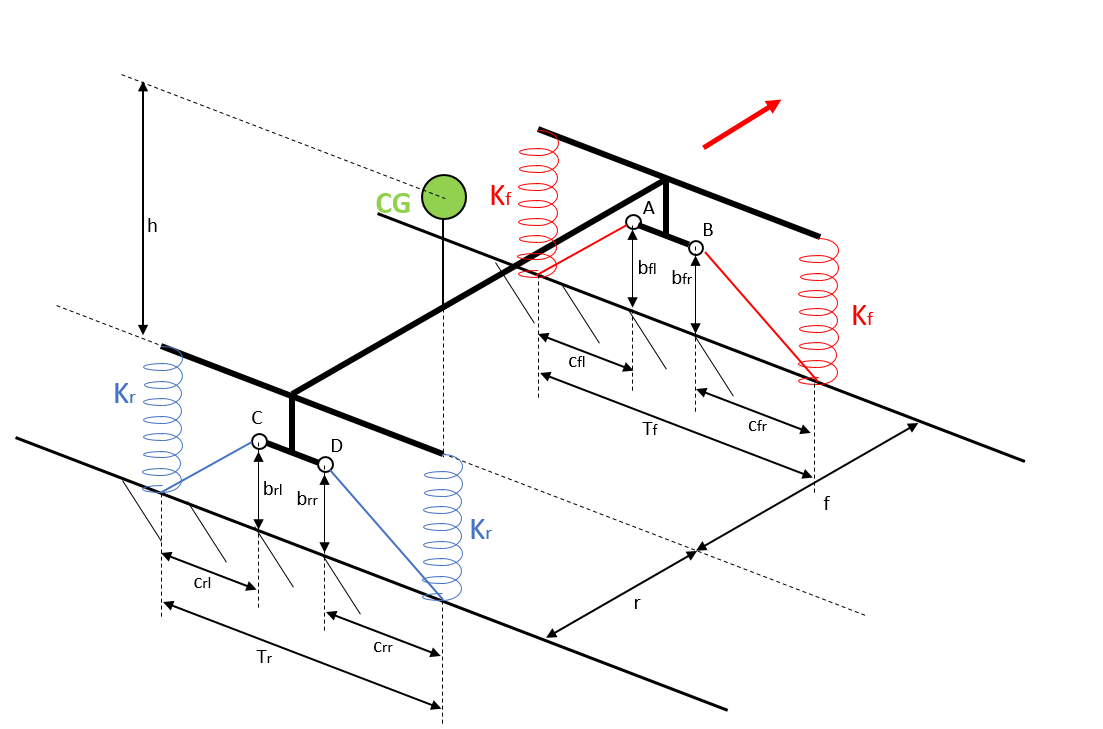
We will consider a simplified vehicle as shown in the following picture, where also all the main dimensions are shown. The chassis is represented by the thick black lines, at which the suspensions, in the form of swing arms, are connected through ball joints. Front suspension arms are shown in red, while rear ones are in blue. Said swing arms connect the contact patch to the chassis, so their constraints to the chassis are simplified representations of the Instant Centers we introduced in our previous entries. In the picture we identify these points as A, B, C and D.
Kf and Kr are respectively front and rear wheel rates in roll, calculating considering springs, antiroll bars and tyres stiffness. The CG seats at a height “h” above the ground and at a distance “f” from the front axle and “r” from the rear.
Front and rear track width are tf and tr respectively. The terms named b and c identify the vertical and lateral distance of suspension ball joints / IC to the contact patch. The astute reader can already recognize the connection between these values and the n-lines slope.
The red arrow indicates the forward direction of motion of our car.
Front and rear roll stiffness can be calculated as previously shown:

In the following picture, the same vehicle model is shown, this time including all the external forces acting on the car. Beside the centrifugal force –mAy and the vertical force Fz (combination of both weight and downforce, with the car here assumed having the CoP at the same position as the CG, for the sake of simplicity) acting at the CG (we ignore aerodynamic drag as it doesn’t conceptually influence what we want to show), we have the four contact patches forces, decomposed in their lateral and vertical components: front left tire force, Ffl (composed by Fyfl and Fzfl), front right tire force, Ffr (composed by Fyfr and Fzfr), rear left tire force, Frl (composed by Fyrl and Fzrl) and rear right tire force, Frr (composed by Fyrr and Fzrr).

If we consider the equilibrium of the vehicle (in lateral and vertical direction and to the rotation around longitudinal axis) we can write the following three equations:

Since we know that:
![]()
where ΔFzf is front load transfer and Fzf0 is the static weight acting on each front tyre (the CG is assumed lying on the car centerline, so the static loads acting on each wheel of the same axle are equal), we can derive:
![]()
And hence:

where ΔFzr is rear load transfer.
So we can conclude:
![]()
To derive front and rear load transfers, we can consider the rotational equilibrium of each suspension, indicated in our schematic representation by each swing arm. To start, we will consider the front left suspension, shown in the left portion of the following picture. Please consider that the violet arrows represent here the variation of spring force (Fsf) magnitude due to load transfer, with respect to static conditions.

The rotational equilibrium of the front left suspension will be given by:![]()
This can be rewritten as:

Analogously, the rotational equilibrium of the right suspension can be expressed as:

As we have seen, front axle roll stiffness is given by:
![]()
We also know that:
![]()
where Δsf is the suspension wheel travel. Combining the two equations we can derive:

Where Φ is car’s roll angle.
Front left and right suspension rotational equilibrium can then be rewritten as:

Summing the two equations together, we obtain:

And hence (using also the same approach for the rear suspension):

Till now, the roll angle remains unknown. Anyway we can calculate it as follows:

where:
![]()
Mroll can be derived considering the equilibrium of the forces applied to the chassis by the control / swing arms.

We know that:

Chassis rotational equilibrium can then be written as:

Hence we derive:

With this in mind we can finally obtain:

These two equations allow to calculate the load transfer that each axle experiences, basing on the cornering force that each tyre of an axle exchange with the road. Some readers may have already recognized how the terms “b/c” multiplying each Fy are nothing else than the slope of the n-line of each suspension. As we said already, n-lines slopes are closely related to the concept of roll centers and, from a pure conceptual perspective, they are nearly synonyms.
The first term of the equation is what we initially called “elastic load transfer”, because its value depends on the roll stiffness contribution of each axle to the overall roll stiffness and, hence, on the elastic elements of the suspension (tyres, springs and antiroll bar). It shows how, increasing the roll stiffness of only one axle produces a bigger load transfer on that axle, because the ratio between that axle roll stiffness and overall roll stiffness will increase. In steady state, this means that, increasing front roll stiffness we will create more understeer (or less oversteer).
The second term is what we initially defined as geometric load transfer. It basically shows how, if the n-line of a suspension gets a bigger slope, as identified by the term “b/c” (or, in other terms, we increase roll center height), the axle under analysis will experience a bigger load transfer. Again, this means if we increase the height “b” of our front pivot points while “c” stays the same (thus increasing our front roll center height), we will create more understeer (or less oversteer).
Out of ΔFzf and ΔFzr we can easy calculate the Total Lateral Load Transfer Distribution (TLLTD):

As we have seen, the bigger the TLLTD, the more the car will tend to understeer in steady state.
For the readers who are more familiar with vehicle dynamic topics, this formulation generates exactly the same results as the one using roll centers, under the same assumptions (cornering forces having the same magnitude on each side of the same axle and summing up to generate simply a Fyf for the front and a Fyr for the rear). Anyway, the equations we wrote are more generic and allows to obtain useful results also when considering non-equal cornering forces on the two side of the same axle (in extreme cases a wheel could be in the air, for example and hence produce no lateral force) or even when facing situations where the roll center migrates to very unpractical locations. This means, this formulation should suite better any coding approach to lateral load transfer calculations.
















