After we introduced tyres and aerodynamics in our first two-article series, we now have the basics we need to look briefly at what happens when a racecar moves on the road.
In general, racecars are vehicles that move often under high accelerations, as the aim of the driver is to get as close as possible to vehicle’s limits. Consequently, increasing the maximum accelerations that the car can explore is a key in improving its lap times and, as we will see, this is strictly connected to how much “grip” the car has in every driving condition.
We will, once again, only scratch the surface about how a car behaves on the road during straight line and cornering motion and we will accept some simplifying assumptions, in order not to make the articles too complex (or boring).
As we will see, aerodynamic downforce is key in increasing the forces that each tyre can exchange with the road in given track conditions, while drag always acts against the powertrain while accelerating. There are other parameters that influence both how much grip the car has and how it behaves, some of them being strongly influenced by the rulebook.
We will start our short analysis with straight line motion, including braking and we will then move on to cornering manoeuvres. Inevitably, we will also shortly mention how certain systems, like suspension, interact with each other also allowing to tune car’s handling, up to a point.
This series of article will inevitably contain some more math and equations than the previous ones, as this is necessary to describe what happens in certain situations. Hopefully, I will succeed in keeping it as simple as possible and to explain clearly enough what is going on in each situation. Nonetheless, a bit of mathematic actually helps to get a feeling about why and how certain physical phenomena take place.
Straight Line Motion
As we mentioned, racecars move in straight line mainly accelerating or braking, at least if we exclude special situation, like driving through the pitlane or under “Full Course Yellow” (race neutralization) conditions.
This means that, in general, racecars speed changes constantly. This is why, if we want to analyze how a race vehicle behaves physically, we will have to discuss how it exchange forces with the road that allow it to accelerate at a certain rate: acceleration is, from a mathematical perspective, nothing but a speed change in time, at least if we consider a pure straight line motion.
According to Newton’s laws, acceleration and force are strictly related to each other and what we aim to understand is exactly which forces a racecar develops in order to accelerate or brake at a certain rate.
Let’s consider a car with a mass “m”, moving with an acceleration “Ax” (whose direction and magnitude we consider, for the sake of simplicity, to stay constant in time). In order to move with the acceleration Ax, the car will have to receive an overall force at the driven wheels contact patches, with a magnitude big enough to overcome the aerodynamic forces, each tyre rolling resistance and the inertial force given by the mass multiplied by the acceleration itself.
As anticipated, we will ignore some of the phenomena taking place when a car accelerates in a straight line, like for example effects connected to wheels angular acceleration. This is a pretty crude approximation, but help us to keep this analysis simple and to concentrate on high-level aspects.
Also, we will assume that the car travels on a perfectly level surface and that there is symmetry between what happens to the left and right wheels of the same axle.

We will focus our attention on an instant where the car moves with a forward velocity “V”.
To analyze what happens, physically, allowing the car to move forward with an acceleration “Ax”, as shown in the above picture, we have to sum all the forces acting on the car.
If we focus on the horizontal components of our vectors (denoted with the subscript “x” in the picture and linked to the overall longitudinal acceleration of the complete vehicle), we see that the only force pushing the car forward is Fpow.
This is the force that the ground applies on the car at the two rear tyres contact patches (at least if we assume the car being rear wheel driven) and is reacted by the torque produced by the engine. This force pushes the car forward, allowing to overpower the resisting forces and to accelerate. The magnitude of this force depends, on one side, on the torque/power that the engine produces and on the other side, on the grip made available by the tyres in their interaction with the road. As we will see, this is the reason why it is much easier to see wheels spinning at low speed than at high speed.
Above all for cars with significant downforce, at low speed the vertical load acting on the driven wheels is lower (among others, because the aerodynamic downforce is lower), determining a lower grip for the tyres. The torque that the engine can supply at the wheel is much higher than what the grip would allow without wheel spin, because of the short gear ratios that we have in first or second gear (we will come to the effect of gear ratios and gearbox in other articles), that multiplies the torque produced by the engine.
This means that the force produced by the engine is bigger than the one produced by the tyres and the wheels start to spin. We can then describe such a situation as “grip limited” because the magnitude of the Ax vector is dictated by how much grip the tyres can ensure. In other words, in such a situation the tyres are the bottleneck: if we had more grip, we could make the acceleration magnitude bigger.
In other conditions (like for example accelerating out of a high-speed corner), the grip produced by the tyres could be bigger than the tractive force delivered by the engine (because of downforce and of the lower torque that the engine can transmit to the driven wheels). In such a situation, we will say that the maximum achievable acceleration is “power limited” because if we would have more power, we could increase its magnitude.
In our picture above, the horizontal forces acting against Fpow are:
- Fxf and Fxr, which are respectively front and rear tyres rolling resistance (here both tyres of each axle).
- Fx, the aerodynamic drag, considered here applied at the CP (Center of Pressure). This point (we spoke about it in our articles about racecars aerodynamics) seats in general in a different position than the CG (car’s Center of Mass, also called Center of Gravity).
It depends on the forward velocity V (assuming no wind) squared, as we saw, again, in our aerodynamic introduction.
It follows that to have an acceleration Ax, we will need a Fpow given by the following equation:
![]()
Aerodynamic drag becomes more and more dominant as the speed increases because it depends on the square of car relative velocity with respect to air (so, assuming no wind, it depends on the square of car speed).
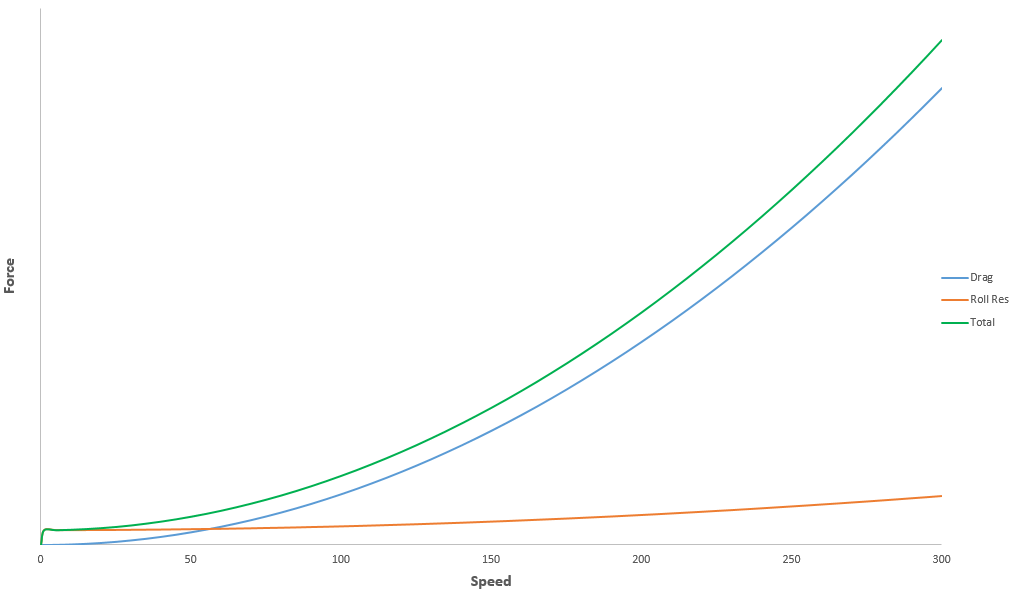
The picture above shows the contribution to the overall resisting force of aerodynamic drag and rolling resistance, for a high downforce car, like an LMP. We recognize rolling resistance becoming a relatively small contribution as the speed increases, with drag becoming the dominant action already above 60-70 km/h.
Drag grows with the square of car speed. What is interesting to notice is that also the rolling resistance has a quadratic curve with respect to car speed, because here we assume its magnitude being a fixed portion of the vertical load acting on the four tyres. Since downforce also depends on the square of car speed (and, hence, so does the vertical load experienced by each tyre), rolling resistance also grows with the square of forward velocity.
Assuming that calculating the rolling resistance as a portion of the vertical load acting on the tyre is a reasonable approach, the sum of the rolling resistances acting on the four wheels can be estimated using the following equation, where we suppose that the rolling resistance coefficient rs has the same value for each of the four tyres:
![]()
Rolling resistance coefficient rs normally has a value of a few percentage points, as we have seen during our tyres overview.
All of this tells us that, given a car with a certain mass and powertrain, aerodynamic drag has the strongest influence in determining a racecar top speed and how much time is needed to cover a certain distance in a straight line.
















