[su_list icon=”icon: angle-double-right” icon_color=”#3498db”]
[/su_list]
In the previous article, we analyzed the basics of a car straight line motion, we introduced the forces involved and we described more in detail all the longitudinal actions, those being more related to how quick a car can travel down a straight track portion. We can now simulate a car travelling in straight line with a simple excel sheet and try to understand how much of an influence a certain change on drag has on car performance.
We will consider a car with features comparable to an LMP2 vehicle and we will analyze its performance on a 1000 m long straight, with the car accelerating from a speed of 100 km/h.
The first case will consider a baseline configuration, while the second one will analyze a car with 10% more drag.
We will assume that car speed stays constant during gear changes. This is, of course, an approximation, but since a racecar normally changes gear very quickly, this is not too far from reality.
The first important result is the time that our vehicle model needs to cover the chosen straight, starting at the given speed, in the two drag configurations. In the baseline case, our car takes about 0.15 seconds less than in the second case, with a difference in top speed of about 6.4 km/h.
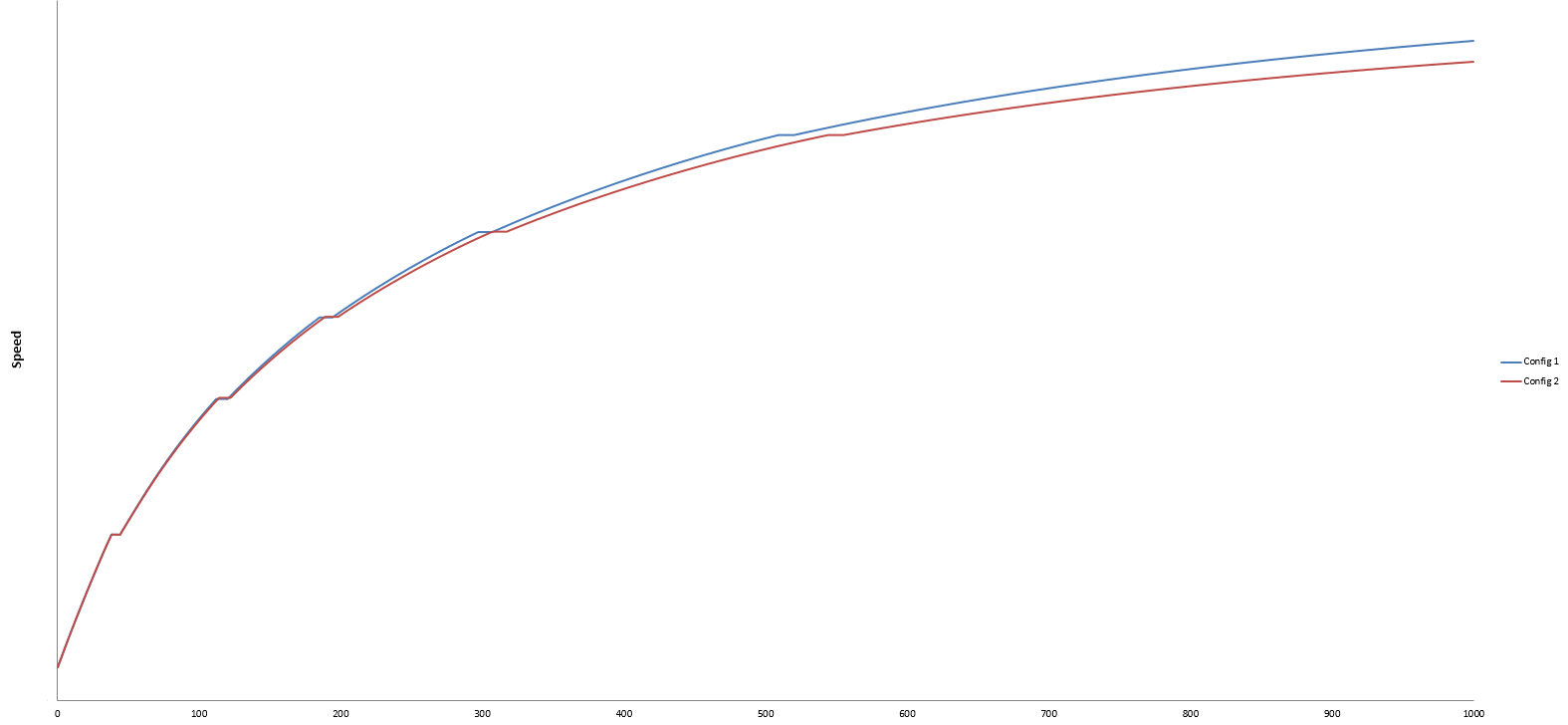
The plot above shows the car’s speed in the two cases (blue is the baseline, red the higher drag configuration) with respect to the travelled distance. The speed difference between the two cases gets bigger as the forward velocity increases because drag effects grow with the square of forward velocity.
Up to about 140 km/h, the car is in a “grip limited” situation and the driver cannot open the throttle completely if he wants to avoid a wheel spin.
This is shown in the following plot, relative to throttle position (from o to 100%), where we can identify how the throttle cannot be held at 100% opening at the beginning of the acceleration phase.

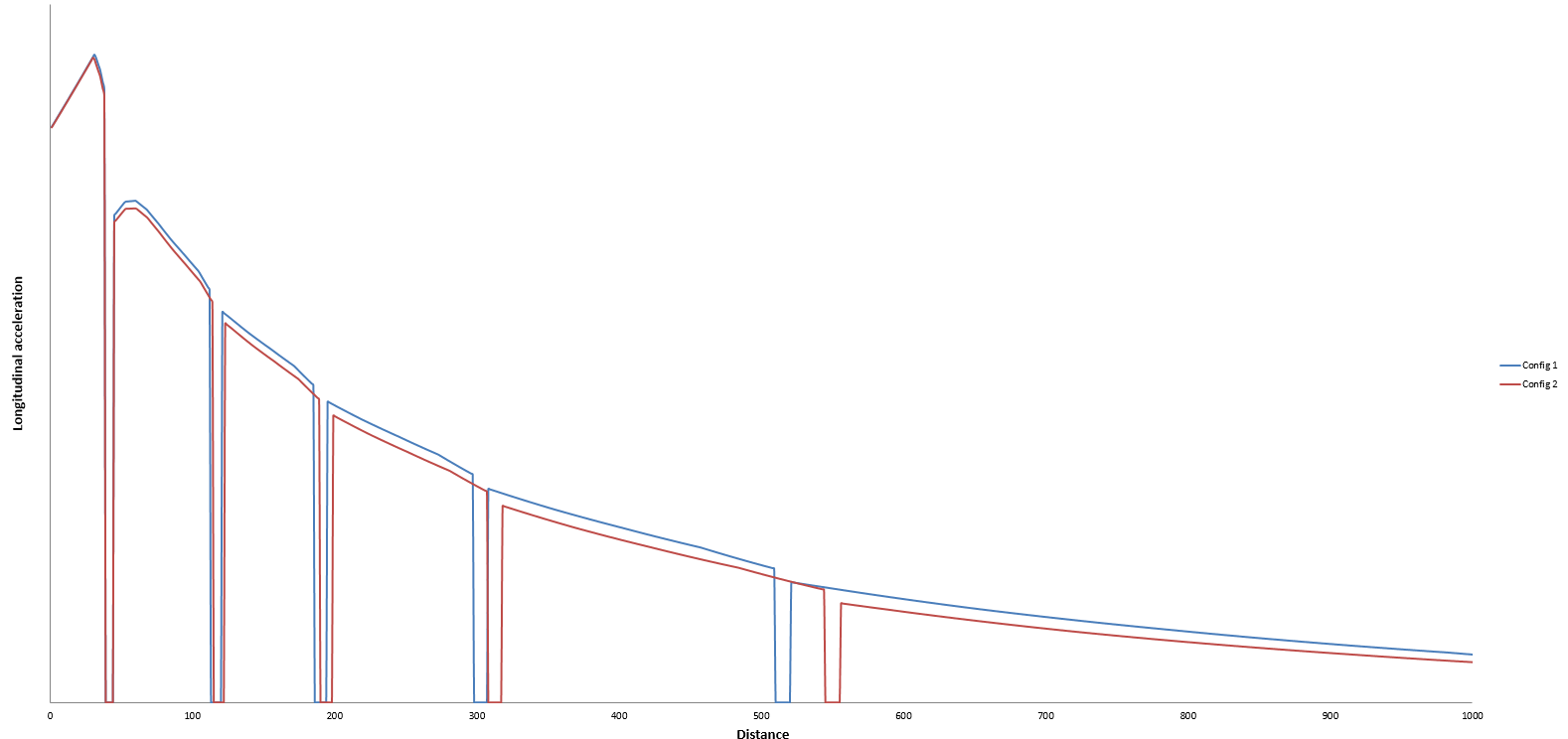
It is also very interesting to take a look at the plot of the longitudinal acceleration with respect to the covered distance. As we can see in the following picture, as the speed increases, the gap between the two cases grows as well, with the gear changes (identified by the regions where the acceleration drops to zero) also happening later in the high drag case, because of the car requiring more time to reach the gear change point.
The acceleration Ax induces an inertial force, given by –mAx, as stated by Newton’s second law. This force is applied to the Center of Mass of the car (normally identified as CG) and, since this point seats above the ground, it will create a moment that increases the vertical load acting on the rear tyres and decrease the vertical load acting on the front ones, compared to a situation where no Ax is acting. The opposite would happen in a braking situation, with the acceleration Ax pointing backwards and the inertial force creating a moment that increases the vertical load acting on the front tyres and decreases the load acting on the rear ones, compared to a situation where Ax has a magnitude equal to zero.
This phenomenon is normally called “load transfer” and its intensity depends on three factors: Ax magnitude, CG height (distance from the ground) and car wheelbase.
Said l car wheelbase and h its CG height, the moment of the inertial force and the load transfer can be calculated respectively with the two following equations:
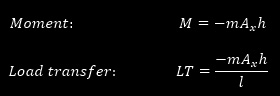
The following picture helps to visually identify all the parameters influencing load transfer.

Load transfer has a great importance in vehicle dynamics, because it is one of the factors influencing the vertical load acting on a tyre and, hence, its grip. Also, as we will see dealing with cornering, it is one of the best tools that a race engineer has to tune his car.
We briefly dealt with it when we introduced tyres in our first series of articles. In general, we can say that weight transfer reduces the overall grip of a car. More precisely, if we consider longitudinal weight transfer, it will increase the maximum magnitude of the forces that an axle can produce, but reduce more sensibly the ones that the other axle can exchange with the road. This is why a lot of effort is invested in trying to build cars with a CG seating as low as possible. Only in very few cases, a designer would lightly accept a compromise on this point and this is when sacrificing something in terms of CG height would produce a bigger advantage in another area (for example aerodynamics) or if it would enable to make the car reliable when otherwise not possible.
If we consider a car accelerating on a straight line, longitudinal weight transfer will produce a bigger load acting on the rear tyres; if the car is rear driven, this actually helps in getting a bigger force exchanged by the rear tyres with the road and, hence, a bigger longitudinal acceleration, at least in grip limited situations. With a front or all-wheel driven car, the unloading effect produced on the front tyres deteriorate overall car grip.
On the other hand, in braking situations, the load transfer will tend to load the front tyres more, while unloading the rear ones. As a consequence, the front tyres will produce a higher grip than the rears and this is why, in general, most of the cars have bigger brakes at the front than at the rear, in order to produce bigger grip torques at the front and to handle the higher stress. In extreme cases, anyway, this could produce such a grip reduction at the rear axle thus to make the car unstable in braking phases, with the rear tyres coming close to or locking. This is easier to experience with GT and touring cars, whose CG seats higher, thus producing a bigger load transfer and have less downforce.
A consequence of load transfer is also a bigger force acting on an axle (or a side) suspension. Since every suspension has some form of elastic elements (like springs, for example) that react to a load deforming or changing their length, load transfer will lead to the car changing its attitude, or the angle the body forms with the ground plane (up to a point, as we will see when dealing with suspension geometry).
This can be sometimes seen as a car brakes hard approaching a corner (it is actually easier to detect with GT cars, as their elastic elements are generally less stiff): the nose will drop, reducing front ride height and, often, increasing the rear. This has an effect also on cars aerodynamics performance; as we saw in our articles about racecars aerodynamics, the aerodynamic forces that a car produces are strongly dependent in its ride heights.

One very important concept, which is sometimes misunderstood, is the relationships between weight transfer and body/suspension motions. As we have seen, anytime there are forces acting at tyres contact patch, car CG will experience an inertial force; since the CG lies above the ground, this will generate a moment and, hence, a weight transfer. The said moment is the cause of any body motion. This means the cause-effect chain looks more or less like this:
Forces at contact patch > Acceleration > Inertial force at the CG > Moment > Weight transfer > Body motion
Any body motion is always a consequence of the main action, namely a force being exchanged by the car with the road; the magnitude of body motion, anyway, depends also on other factors, like suspension stiffness and geometry.
















